题目链接点击这里

Problem Description

It's said that Aladdin had to solve seven mysteries before getting the Magical Lamp which summons a powerful Genie. Here we are concerned about the fourth mystery.

In the cave, Aladdin was moving forward after passing the pathway of magical stones. He found a door and he was about to open the door, but suddenly a Genie appeared and he addressed himself as the guardian of the door. He challenged Aladdin to play a game and promised that he would let Aladdin go through the door, if Aladdin can defeat the Genie. Aladdin defeated the Genie and continued his journey. However, let's concentrate on the game.

The game was called 'Game of Bracelets'. A bracelet is a linear chain of some pearls of various weights. The rules of the game are:

1. There are n bracelets.
2. Players alternate turns.
3. In each turn, a player has to choose a pearl from any bracelet. Then all the pearls from that bracelet, that were not lighter than the pearl, will be removed. It may create some smaller bracelets or the bracelet will be removed if no pearl is left in the bracelet.
4. The player, who cannot take a pearl in his turn, loses.

For example, two bracelets are: 5-1-7-2-4-5-3 and 2-1-5-3, here the integers denote the weights of the pearls. Suppose a player has chosen the first pearl (weight 5) from the first bracelet. Then all the pearls that are not lighter than 5, will be removed (from first bracelet). So, 5-1-7-2-4-5-3, the red ones will be removed and thus from this bracelet, three new bracelets will be formed, 1, 2-4 and 3. So, in the next turn the other player will have four bracelets: 1, 2-4, 3 and 2-1-5-3. Now if a player chooses the only pearl (weight 3) from the third bracelet, then the bracelet will be removed.

Now you are given the information of the bracelets. Assume that Aladdin plays first, and Aladdin and the Genie both play optimally. Your task is to find the winner.

Input

Input starts with an integer T (≤ 50), denoting the number of test cases.

Each case starts with a line containing an integer n (1 ≤ n ≤ 50). Each of the next n lines contains an integer Ki (1 ≤ Ki ≤ 50) followed by Ki integers, denoting the weights of the pearls of the ith (1 ≤ i ≤ n) bracelet. Each weight will lie in the range [1, 105].

Output

For each case, print the case number and 'Aladdin' if Aladdin wins. Otherwise print 'Genie'. If Aladdin wins, then print an additional line, denoting the weight of pearls, one of which should be chosen in the first move by Aladdin such that he can win. Each pearl should be denoted by a pair of integers: the first integer is the bracelet number and the second integer is the weight. Sort the pearls first by the bracelet number then by the weight. And same weight in a bracelet should be reported once. Check the samples for exact formatting.

Sample Input

4
2
7 5 1 7 2 4 5 3
4 2 1 5 4
2
2 5 2
2 5 2
1
5 5 2 5 2 5
3
5 5 2 5 2 5
5 7 2 7 3 2
4 5 1 5 4

Sample Output

Case 1: Aladdin
(2 5)
Case 2: Genie
Case 3: Aladdin
(1 2)(1 5)
Case 4: Aladdin
(2 7)(3 1)(3 5)

题意

现在有几串手镯，每个手镯上都有一些珠子，每个珠子都有权值，Aladdin 和 Genie 轮流取珠子，当取了一颗珠子后，这个手镯上所有权值大于等于这颗珠子权值的珠子，都要被删去。因此，这个手镯就会变成新的几个手镯（因为被切割了）。

如，5-1-7-2-4-5-3 这串手镯，选第一颗珠子，权值为5，因此，5，7，5 就要被删去。手镯变成了新的 1，2-4，3 三个手镯。

题解

每个手镯都是独立的，因此可以异或每个手镯的 sg 值求解。而每个手镯，可以在某些结点被取走珠子，变成新的几段，任意一种情况的 sg 值，便是新分成的几段的 sg 值异或起来。再将每一种情况的 sg 值，记录在 vis 中，查找没出现过的最小的值，便是这个手镯的 sg 值。有点绕，我写的时候也有点迷了。

因为范围较小，可直接暴力查找每一段的 sg 值。用记忆化搜索，重复找过的就不找了。sg[i][j] 代表当前这个手镯，左端点下标为 i ，右端点下标为 j ，当找过这一段的 sg 值时，便直接返回不再重复找。

下面举一个例子...我们求 sg[1][4]，即左端点下标为 1，右端点下标为 4:

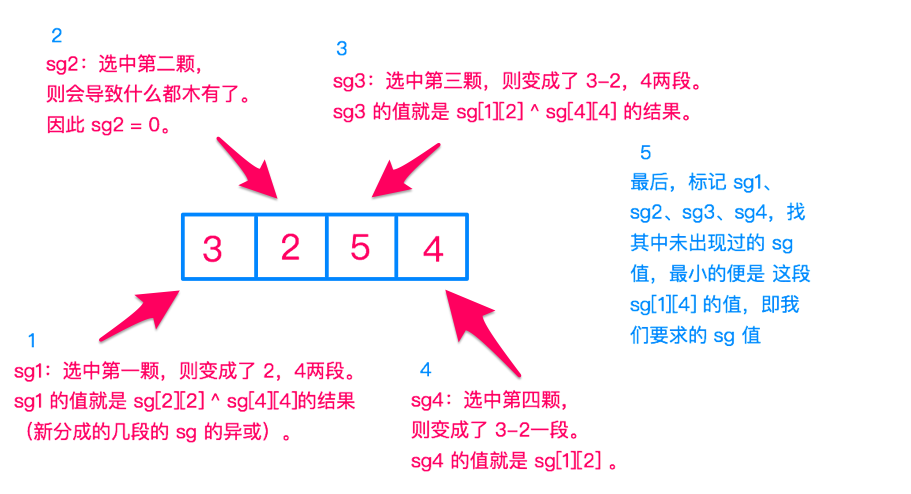
最后的结果，是将每个手镯的 sg 值异或，若为 0 ，则后手赢，否则先手赢。

若先手赢，还需输出第一次赢怎么取。
换位思考一下即可。我们需要先手取完，后手取的时候，面临一个所有手镯的 sg 值异或为 0 的情况（这样的情况是后手赢，此时后手是先手）。

因此，直接暴力枚举每个手镯的每个珠子。看取完后，原本的手镯的 sg值异或，再异或被选中的这个手镯，取走一部分珠子后的 sg 值。

code

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 55;
int sg[maxn][maxn]; // 当前手镯 i-j区间的 sg 值
int arr[maxn][maxn], num[maxn]; // 存储每个手镯的权值，每个手镯有多少个珠子
int sgtmp[maxn]; // 第 i 个手镯的 sg 值
int ret[maxn][maxn];  // 去掉第 i 个手镯的第 j 个珠子后，这个手镯的 sg 值

struct node {
    int x, y;
} output[maxn * maxn]; // 存储最后的输出答案

bool operator == (node a, node b) {
    return a.x == b.x && arr[a.x][a.y] == arr[b.x][b.y];
}

bool cmp(node a, node b) {
    if (a.x == b.x) {
        return arr[a.x][a.y] < arr[b.x][b.y];
    }
    return a.x < b.x;
}

int dfs(int now, int l, int r) { // 查找 sg 值
    if (l > r) return 0;
    if (l == r) return sg[l][r] = 1; // 只有一颗珠子，直接取走，必赢
    
    if (sg[l][r] != -1) return sg[l][r]; // 已找过

    int vis[maxn]; // 不可为全局变量
    memset(vis, 0, sizeof(vis));
    
    for (int i = l; i <= r; ++i) { // 挑选下标为i处的珠子
        int tmp = 0, last = -1;

        // 找到第一颗小于当前权值的珠子
        for (int j = l; j <= r; ++j) {
            if (arr[now][j] < arr[now][i]) {
                last = j; break;
            }
        }
        
        // last 为 -1时，代表已找不到
        for (int j = last + 1; j <= r && last != -1; ++j) {
            if (arr[now][j] >= arr[now][i]) {
                tmp ^= dfs(now, last, j - 1);
                last = -1;
                for (int k = j + 1; k <= r; ++k) {
                    if (arr[now][k] < arr[now][i]) {
                        last = j = k;
                        break;
                    }
                }
            }
        }
        // 这个手镯的最后一段没被搜索
        if (last != -1) {
            tmp ^= dfs(now, last, r);
        }
        vis[tmp] = 1;
        // 记录下来，方便后面输出
        if (l == 1 && r == num[now]) ret[now][i] = tmp;
//        if (l == 1 && r == num[now]) {
//            printf("%d %d %d\n", now, i, tmp);
//        }
    }
    
    for (int i = 0; ; ++i) {
        if (vis[i] == 0) {
            sg[l][r] = i;
            return i;
        }
    }
    return -1;
}

int main() {
    int t, k, ca = 1;
    scanf("%d", &t);
    while (t--) {
        int ans = 0;
        scanf("%d", &k);
        for (int i = 1; i <= k; ++i) {
            memset(sg, -1, sizeof(sg));
            scanf("%d", &num[i]);
            for (int j = 1; j <= num[i]; ++j) {
                scanf("%d", &arr[i][j]);
            }
            sgtmp[i] = dfs(i, 1, num[i]);
            //printf("%d\n", sgtmp[i]);
            ans ^= sgtmp[i];
//            for (int i = 1; i <= num[i]; ++i) {
//                for (int j = i; j <= num[i]; ++j) {
//                    printf("%d %d %d\n", i, j, sg[i][j]);
//                }
//            }
        }
        if (ans == 0) printf("Case %d: Genie\n", ca++);
        else {
            int cnt = 0;
            printf("Case %d: Aladdin\n", ca++);
            memset(output, 0, sizeof(output));
            for (int i = 1; i <= k; ++i) {
                for (int j = 1; j <= num[i]; ++j) {
                    // 先异或这个手镯的 sg 值，消除原本的影响
                    // 再异或这个手镯选中第j颗珠子，导致取走一部分珠子后的sg值
                    if ((ans ^ sgtmp[i] ^ ret[i][j]) == 0) {
                        //printf("(%d %d)", i, arr[i][j]);
                        output[cnt++] = {i, j};
                    }
                }
            }
            // 排序并去重，输出
            sort(output, output + cnt, cmp);
            cnt = (int)(unique(output, output + cnt) - output);
            for (int i = 0; i < cnt; ++i) {
                printf("(%d %d)", output[i].x, arr[output[i].x][output[i].y]);
            };
            printf("\n");
        }
    }
    return 0;
}