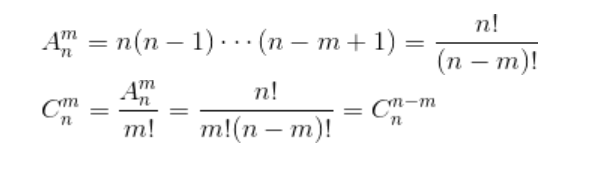本来存在电脑上的...怕有一天电脑突然炸了...所以博客上再备份一份

[队列]
priority_queue<int, vector<int>, greater<int> > q; // 从小到大

[最长公共子序列]

#include <iostream>
#include <cstring>
using namespace std;

int a[1010];
int b[1010];

int l[1010][1010];

int main() {
    
    int n, m;
    while (cin >> n >> m) {
        for (int i = 1; i <= m; ++i) {
            scanf("%d", &a[i]);
        }
        for (int i = 1; i <= m; ++i) {
            scanf("%d", &b[i]);
        }
        memset(l, 0, sizeof(l));
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= m; ++j) {
                if (a[i] == b[j]) {
                    l[i][j] = l[i-1][j-1] + 1;
                } else {
                    l[i][j] = max(l[i-1][j], l[i][j-1]);
                }
            }
        }
        cout << l[m][m] << endl;
    }
    return 0;
}

[最长下降子序列]

#include <iostream>
using namespace std;
// 最长下降子序列
int arr[20010];
int m[20010];

int main() {
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        for (int i = 0; i < n; ++i) {
            scanf("%d", &arr[i]);
        }
        m[0] = 1;
        int max_num = 1;
        for (int i = 1; i < n; ++i) {
            int tmp = 0;
            for (int j = 0; j < i; ++j) {
                if (arr[i] <= arr[j]) {
                    tmp = max(tmp, m[j]);
                }
            }
            m[i] = tmp + 1;
            max_num = max(max_num, m[i]);
        }
        cout << n - max_num << endl;
    }
    
    return 0;
}

[01背包裸题]

#include <iostream>
#include <cstring>
using namespace std;

int v[10010];
int w[10010];
int dp[10010];

int max(int a, int b) {
    return a > b ? a : b;
}

int main() {
    int bag, n;
    while (cin >> bag >> n) {
        for (int i = 1; i <= n; ++i) {
            scanf("%d", &v[i]); //体积
        }
        for (int i = 1; i <= n; ++i) {
            scanf("%d", &w[i]); // 价值
        }
        memset(dp, 0, sizeof(dp)); // 必须要
        for (int i = 1; i <= n; ++i) {
            for (int j = bag; j >= v[i]; --j) {
                dp[j] = max(dp[j], dp[j-v[i]] + w[i]);
            }
        }
        cout << dp[bag] << endl;
    }
    return 0;
}

[完全背包]

#include <iostream>
#include <cstring>
using namespace std;

int v[1010];
int w[1010];
int dp[10010];

int main() {
    int n, bag;
    while (cin >> n >> bag) {
        dp[0] = 0;
        for (int i = 1; i <= n; ++i) {
            scanf("%d%d", &w[i], &v[i]);
        }
        for (int i = 1; i <= bag; ++i) {
            dp[i] = -2000000; // 负无穷，要求装满，否则等于0
        }
        for (int i = 1; i <= n; ++i) {
            for (int j = v[i]; j <= bag; ++j) {
                dp[j] = max(dp[j], dp[j-v[i]] + w[i]);
            }
        }
        cout << dp[bag] << endl;
    }
    return 0;
}

[多重背包]

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

int v[2010];
int w[2010];
int num[1010];
int dp[20005];

int main() {
    int t, n, bag;
    cin >> t;
    while (t--) {
        cin >> bag >> n;
        memset(dp, 0, sizeof(dp));
        for (int i = 1; i <= n; ++i) {
            scanf("%d%d%d", &v[i], &w[i], &num[i]);
        }
        
        int k = n + 1;
        for (int i = 1; i <= n; ++i) {
            int d = 1;
            while (num[i] > d) {
                v[k] = d * v[i];
                w[k++] = d * w[i];
                num[i] -= d;
                d *= 2;
            }
            v[i] *= num[i];
            w[i] *= num[i];
        }
        for (int i = 1; i < k; ++i) {
            for (int j = bag; j >= v[i]; --j) {
                dp[j] = max(dp[j], dp[j-v[i]] + w[i]);
            }
        }
        cout << dp[bag] << endl;
        
    }
    return 0;
}

[混合背包]

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

int v[2010];
int w[2010];
int num[1010];
int dp[20005];

int main() {
    int n, bag;
    while (cin >> bag >> n) {
        
        memset(dp, 0, sizeof(dp));
        for (int i = 1; i <= n; ++i) {
            scanf("%d%d%d", &v[i], &w[i], &num[i]);
        }
        
        int k = n + 1;
        for (int i = 1; i <= n; ++i) {
            if (num[i] <= 1) {
                continue;
            }
            int d = 1;
            while (num[i] > d) {
                v[k] = d * v[i];
                w[k++] = d * w[i];
                num[i] -= d;
                d *= 2;
            }
            v[i] *= num[i];
            w[i] *= num[i];
        }
        
        for (int i = 1; i < k; ++i) {
            if (num[i] > 0)  // 01背包/多重背包
                for (int j = bag; j >= v[i]; --j) {
                    dp[j] = max(dp[j], dp[j-v[i]] + w[i]);
                }
            else  // 完全背包
                for (int j = v[i]; j <= bag; ++j) {
                    dp[j] = max(dp[j], dp[j-v[i]] + w[i]);
                }
        }
        cout << dp[bag] << endl;
        
    }
    return 0;
}

[区间dp]

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

int arr[210], a;
long long int dp[210][210];
int sum[210];

int main(int argc, const char * argv[]) {
    int n;
    while (cin >> n) {
        sum[0] = 0;
        for (int i = 1; i <= n; ++i) {
            cin >> a;
            sum[i] = sum[i - 1] + a;
        }
        memset(dp, 0, sizeof(dp));
        for (int len = 2; len <= n; ++len) {
            for (int i = 1; i + len - 1 <= n; ++i) {
                int j = i + len - 1;
                for (int k = i; k < j; ++k) {
                    dp[i][j] = max(dp[i][j], dp[i][k] + dp[k+1][j] + sum[j] - sum[i - 1]);
                }
            }
        }
        printf("%lld\n", dp[1][n]);
    }
    return 0;
}

[左右相关的区间dp]

#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
using namespace std;

int dp[110][110];

int main() {
    string s;
    while (cin >> s && s != "0") {
        memset(dp, 0, sizeof(dp));
        int max_size = (int)s.size();
        for (int len = 2; len <= max_size; ++len) {
            for (int i = 0; i < max_size; ++i) {
                int j = i + len - 1;
                if (j >= max_size) {
                    break;
                }
                
                for (int k = i; k < j; ++k) {
                    dp[i][j] = max(dp[i][j], dp[i][k]+dp[k+1][j]);
                }
                if ((s[i] == '(' && s[j] == ')')
                    || (s[i] == '[' && s[j] == ']')) {
                    dp[i][j] = max(dp[i][j], dp[i + 1][j - 1] + 2);
                }
            }
        }
        
        cout << dp[0][max_size - 1] << endl;
    }
    return 0;
}

[树状dp]

#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
using namespace std;

int arr[6010], par[6010];
int dp[6010][2];
vector<vector<int> > child;

int dfs(int now, int choice) {
    if (dp[now][choice] != -1) {
        return dp[now][choice];
    }
    // now 不选
    if (choice == 0) {
        dp[now][0] = 0;
        for (int i = 0; i < child[now].size(); ++i) {
            dp[now][0] += max(dfs(child[now][i], 0), dfs(child[now][i],1));
        }
    } else {
        // now 选
        dp[now][1] = arr[now];
        for (int i = 0; i < child[now].size(); ++i) {
            dp[now][1] += dfs(child[now][i], 0);
        }
    }
    return dp[now][choice];
}

int main() {
    int n;
    while (cin >> n) {
        for (int i = 1; i <= n; ++i) {
            cin >> arr[i];
        }
        int a, b;
        child.clear();
        child.resize(n + 1);
        memset(par, -1, sizeof par);
        for (int i = 0; i < n - 1; ++i) {
            cin >> a >> b;
            par[a] = b;
            child[b].push_back(a);
        }
        cin >> a >> b;
        // 记忆化搜索的初始化
        memset(dp, -1, sizeof(dp));
        // 边界
        for (int i = 1; i <= n; ++i) {
            if (child[i].size() == 0) {
                // 叶子结点
                dp[i][0] = 0, dp[i][1] = arr[i];
            }
        }
        // 找根节点
        int root = 0;
        for (int i = 1; i <= n; ++i) {
            if (par[i] == -1) {
                root = i;
                break;
            }
        }
        // 搜索
        cout << max(dfs(root, 0), dfs(root, 1)) << endl;
        
    }
    return 0;
}

[归并排序+求逆序对]

#include <iostream>
#include <vector>
#include <cstdio>
#include <cstring>
using namespace std;

int data[10000010];
int tmp[10000010];

long long int cnt;
void Merge(int beg, int mid, int end) {
    if (end <= beg)
        return;
    
    int i = 0;
    int beg1 = beg, beg2 = mid;
    while (beg1 < mid && beg2 < end) {
        if (data[beg1] <= data[beg2]) {
            tmp[i++] = data[beg1++];
        } else {
            tmp[i++] = data[beg2++];
            cnt += mid - beg1;
        }
    }
    while (beg1 < mid) {
        tmp[i++] = data[beg1++];
    }
    while (beg2 < end) {
        tmp[i++] = data[beg2++];
    }
    memcpy(data + beg, tmp, sizeof(int) * (end - beg));
}

int main(int argc, const char * argv[]) {
    
    int n;
    while (cin >> n) {
        cnt = 0;
        for (int i = 0; i < n; ++i) {
            scanf("%d", &data[i]);
        }
        for (int length = 1; length <= n; length *= 2) {
            int beg = 0, mid = beg + length, end = mid + length;
            for(; beg < n; beg += 2 * length,
                           mid = beg + length, end = mid + length) {
                if (mid > n) {
                    mid = n;
                }
                if (end > n) {
                    end = n;
                }
                Merge(beg, mid, end);
            }
        }
        cout << cnt << endl;
    }    
    return 0;
}

[最大连续子序列分治版]

#include <cstdio>
#include <iostream>
using namespace std;

int a[100010];

struct node {
    int sum, left, right;
};

node recursionMax (int left, int right)
{
    // 只有一个数
    if (left == right) return {a[left], left, right};
    
    int mid = (left + right) / 2;
    
    node maxLeft = recursionMax (left, mid); // 左
    node maxRight = recursionMax(mid + 1, right); // 右
    
    int left_sum = -0x7fffffff, right_sum = -0x7fffffff, li = mid, ri = mid + 1;
    int tmp = 0;
    for (int i = mid; i >= left; i--)
    {
        tmp += a[i];
        if (left_sum <= tmp) {
            left_sum = tmp;
            li = i;
        }
    }
    
    tmp = 0;
    for (int  j = mid + 1; j <= right; j++)
    {
        tmp += a[j];
        if (right_sum < tmp) {
            right_sum = tmp;
            ri = j;
        }
    }
    node ret = maxLeft.sum >= maxRight.sum ? maxLeft : maxRight;
    if (ret.sum > left_sum + right_sum) {
        return ret;
    } else if (ret.sum == left_sum + right_sum && ret.left < li) {
        return ret;
        
    } else {
        return {left_sum + right_sum, li, ri};
    }
}

int main ()
{
    int  n;
    while (cin >> n) {
        for (int i = 0; i < n; ++i) {
            cin >> a[i];
        }
        node ret = recursionMax(0, n - 1);
        printf("%d %d %d\n", ret.sum, ret.left + 1, ret.right + 1);
    }
    return 0;
}

[点分治]

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;

struct node {
    double x, y;
} a[100010], b[100010];

bool cmpx(struct node i, struct node j) {
    return i.x < j.x;
}

bool cmpy(struct node i, struct node j) {
    return i.y < j.y;
}

double dis(struct node i, struct node j) {
    return sqrt(pow(i.x - j.x, 2) + pow(i.y - j.y, 2));
}

double find_min(int left, int mid, int right, double s) {
    int count = 0;
    for (int i = left; i <= right; ++i) {
        if (a[i].x >= a[mid].x - s && a[i].x <= a[mid].x + s) {
            // 在中间
            b[count].x = a[i].x;
            b[count++].y = a[i].y;
        }
    }
    sort(b, b + count, cmpy);
    for (int i = 0; i < count; ++i) {
        for (int j = i + 1; j < count; ++j) {
            if (b[j].y - b[i].y > s) {
                break;
            }
            double ret = dis(b[i], b[j]);
            
            if (ret < s) {
                s = ret;
            }
        }
    }
    return s;
}

double recursionMax (int left, int right) {
    if (left >= right) {
        return 0x7fffffff;
    }
    // 只有两个数
    if (left == right - 1) {
        return dis(a[left], a[right]);
    }
    int mid = (left + right) / 2;
    double x;
    if (right - left == 2) {
        x = dis(a[left], a[right]);
        x = min(x, dis(a[mid], a[right]));
        x = min(x, dis(a[mid], a[left]));
        return x;
    }
    double minLeft = recursionMax (left, mid); // 左
    double minRight = recursionMax(mid, right); // 右
    
    double s = minLeft <= minRight ? minLeft : minRight;
    
    s = find_min(left, mid, right, s);
    return s;
}

int main ()
{
    int  n;
    while (cin >> n && n) {
        for (int i = 0; i < n; ++i) {
            cin >> a[i].x >> a[i].y;
        }
        sort(a, a + n, cmpx);
        double ret = recursionMax(0, n - 1);
        printf("%0.2lf\n", ret / 2);
    }
    return 0;
}

[atoi]

#include <stdlib.h>
#include <stdio.h>

int main(void)
{
    int n;
    char *str = "12345.67";
    n = atoi(str);
    printf("n=%d\n",n);
    return 0;
}
输出：
n = 12345

[itoa]（若不能用，可用sprintf）

#include <stdlib.h>
#include <stdio.h>

int main(void)
{
    int number = 123456;
    char string[25];
    itoa(number, string, 10);
    printf("integer=%d string=%s\n”, number, string);
    return 0;
}

[sprintf]

#include <stdio.h> //头文件
int main(void)
{
    int number = 123456;
    char string[25]; // 必须为 char* 类型
    // 参数：数组，以何种形式输出，数字
    sprintf(string, "%d", number);
    printf("integer=%d string=%s\n”, number, string);
    return 0;
}

[gcd 最大公约数]

long long int gcd(long long int a, long long int b) {
    return (b == 0) ? a : gcd(b, a % b);
}

[lcm 最小公倍数]

long long int lcm(long long int a, long long int b) {
    return a * b / gcd(a, b);
}

[大数相加]
参数：
数1：a ，长度：len1
数2：b ，长度：len2
注：
a[0] 也存储数，a 从下标为 0 处开始存储（b相同），且 a 和 b 为顺序存储，即:
数字：123
数组 a：a[0] = 1, a[1] = 2, a[3] = 3;

[code]

void sum_a_b(char a[], char b[], int len1, int len2) {
    int q = 0;
    len1--, len2--; // len1 和 len2 为长度，减 1 后为下标
    int sum[1010], i = 0; // sum 数组存储结果，i 存储 sum 的下标
    while (len1 >= 0 && len2 >= 0) { // 从两数组最后一位开始计算
        sum[i++] = (q + a[len1] + b[len2] - 2 * '0') % 10;
        q = (q + a[len1--] + b[len2--] - 2 * '0') / 10;
    }
    // 若某一个数较长，继续加
    while (len1 >= 0) {
        sum[i++] = (q + a[len1] - '0') % 10;
        q = (q + a[len1--] - '0') / 10;
    }
    while (len2 >= 0) {
        sum[i++] = (q + b[len2] - '0') % 10;
        q = (q + b[len2--] - '0') / 10;
    }
    // 加上进位的 q，若 q 为0 也没关系，下一步会去除 0
    sum[i] = q;
    
    // 若得出的 sum 中开头有过多的0
    while (sum[i] == 0) {
        --i;
    }

    // 这里为输出，需要将 sum 从后往前输出
    for (int j = i; j >= 0; --j) {
        cout << sum[j];
    }
    cout << endl;
}

[数论]
数根：各位数字之和
x 的树根 = (x - 1) % 9 + 1

[图论]
若图中存在这样一条路径，使得它恰通过G中每条边一次,则称该路径为欧拉路径。
若该路径是一个圈，则称为欧拉(Euler)回路。

[图的存储]

定理：

（一）一个图有“欧拉回路”当且仅当它是连通的且每个顶点都有偶数度。

（二）一个图有“欧拉通路”当且经当它是连通的且除两个顶点外，其他顶点都有偶数度。（含奇数度的两个节点中，一个必为欧拉通路起点，另一个必为欧拉通路的终点）

[连通分量]：无向图中的极大连通子图

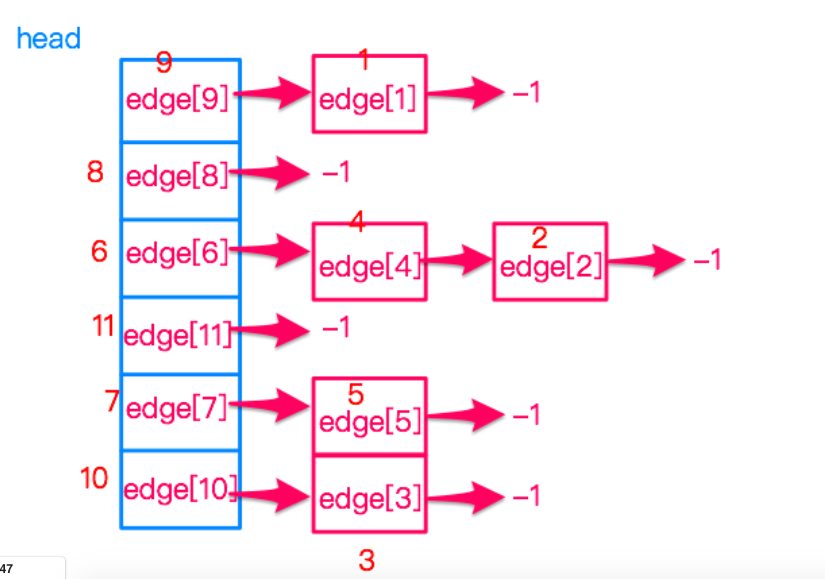
[拓扑排序]

#include <iostream>
#include <cstring>
#include <queue>
#include <cstdio>
using namespace std;
struct node {
    int _to; // 若有权，加一个 int l;
    int _next;
} edge[550];

int num;

int in[550]; // 入度
int ret[550];
int head[550];

void insert(int x, int y) {
    edge[num]._to = y;
    edge[num]._next = head[x];
    head[x] = num++;
}

int main(int argc, const char * argv[]) {
    int n, m;
    while (cin >> n >> m) {
        num = 0;
        memset(head, -1, sizeof(head));
        int x, y;
        for (int i = 0; i < m; ++i) {
            scanf("%d%d", &x, &y);
            insert(x, y);
            ++in[y];
        }
        priority_queue<int, vector<int>, greater<int> > q;
        for (int i = 1; i <= n; ++i) {
            if (in[i] == 0) q.push(i);
        }
        int k = 0;
        while (!q.empty()) {
            int a = q.top();
            ret[k++] = a;
            q.pop();
            for (int now = head[a]; now != -1; now = edge[now]._next) {
                --in[edge[now]._to];
                if (in[edge[now]._to] == 0) {
                    q.push(edge[now]._to);
                }
            }
        }
        for (int i = 0; i < n - 1; ++i) {
            cout << ret[i] << ' ';
        }
        cout << ret[n - 1] << endl;
    }
    return 0;
}

关键路径:从源点到汇点的最长路径长度

dijkstral算法 (复杂度O(n^2))——不能有负权边
spfa算法 (复杂度O(km))——不能有负权环
Floyd (复杂度O(n^3))——可以求多源点最短路

[dijkstra]

#include <iostream>
#include <cstring>
#include <stack>
#include <cstdio>
#include <vector>
using namespace std;

const int inf = 0x3f3f3f3f;
int n, m;
int road[1010][1010];
int vis[1010], dis[1010], pre[1010];

bool dijkstra(int s, int e) {
    vis[s] = 1;
    
    for (int i = 1; i < n; ++i) {
        int minD = inf, k = -1;
        for (int j = 1; j <= n; ++j) {
            if (!vis[j] && dis[j] < minD) {
                minD = dis[j];
                k = j;
            }
        }
        vis[k] = 1;
        
        if (k == e) break;
        if (k == -1) return 0; // 不通
        
        for (int j = 1; j <= n; ++j) {
            if (!vis[j] && dis[k] + road[k][j] < dis[j]) {
                dis[j] = dis[k] + road[k][j];
                pre[j] = k;
            }
        }
    }
    return 1;
}

int main() {
    
    while (cin >> n >> m) {
        int a, b, z;
        for (int i = 1; i <= n; ++i) {
            fill(road[i] + 1, road[i] + n + 1, inf);
        }
        for (int i = 0; i < m; ++i) {
            cin >> a >> b >> z;
            road[a][b] = min(z, road[a][b]); // 有向
            road[b][a] = min(z, road[b][a]); // 无向
        }
        memset(vis, 0, sizeof(vis));
        for (int i = 1; i <= n; ++i) {
            dis[i] = road[1][i];
            pre[i] = 1;
        }
        dis[1] = 0;
        if (dijkstra(1, n) == 0) {
            cout << -1 << endl;
            continue;
        }
        int k = pre[n];
        stack<int> s;
        while (k != 1) {
            s.push(k);
            k = pre[k];
        }
        cout << 1 << ' ';
        while (!s.empty()) {
            cout << s.top() << ' ';
            s.pop();
        }
        cout << n << endl;
    }
    return 0;
}

[FLOYD算法]

 for (int i = 1; i <= 32; ++i) {
        for (int j = 1; j <= 32; ++j) {
            for (int k = 1; k <= 32; ++k) {
                if (i != j && j != k && k != i
                    && dis[i][k] + dis[k][j] <= dis[i][j]) {
                    dis[i][j] = dis[i][k] + dis[k][j];
                }
            }
        }
    }

最小生成树：生成子图是一棵树，且树枝的权值在所有生成树中，总和最小。

prim 算法 (复杂度O(n^2))——适用于稠密图
kruskal算法 (复杂度O(m*lg(m))——适用于稀疏图

/////////////////////////////

对于Prim，其选取的边(u,v)必有一个顶点已经被覆盖，另一个顶点未被覆盖。

Kruskal算法：先将所有的边做排序，然后利用并查集作判断来优先选择较小的边，直到建成一棵生成树。对于Kruskal,其选取的边(u,v)任意，只要这个边的加入不能使被覆盖的顶点构成回路。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

struct node {
    int x, y, l; // 起点 重点 长度
} edge[1010];

int a[1010], b[1010], fa[1010];

bool cmp(node x, node y) {
    return x.l < y.l;
}

int findfa(int x) {
    return fa[x] == x ? x : (fa[x] = findfa(fa[x]));
}

void merge(int i, int j) {
    fa[findfa(i)] = findfa(j);
}

long long int kruskal(int num) {
    int cnt = 0;
    long long int sum = 0;
    for (int i = 0; i < num; ++i) {
        int fx = findfa(edge[i].x);
        int fy = findfa(edge[i].y);
        if (fx != fy) {
            merge(fx, fy);
            ++cnt;
            sum += edge[i].l;
            if (cnt >= num - 1) {
                break;
            }
        }
        
    }
    return sum;
}

int main() {
    int n;
    while (cin >> n) {
        for (int i = 1; i <= n; ++i) {
            fa[i] = i;
        }
        for (int i = 1; i <= n; ++i) {
            cin >> a[i] >> b[i];
        }
        int num = 0;
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (i != j) {
                    edge[num].x = i;
                    edge[num].y = j;
                    edge[num++].l = a[i] * b[j] + a[j] * b[i];
                }
            }
        }
        sort(edge, edge + num, cmp);
        cout << kruskal(num) << endl;
    }
    return 0;
}